-
经公安部交管局统计,今年5月份全国因道路交通事故造成伤亡共25591人.这个数据用科学记数法可以表示为( )
A.2.5591×105
B.25.591×103
C.2.5591×104
D.2.5591×106难度: 中等查看答案及解析
-
某纺织厂从10万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么估计该厂这10万件产品中合格品约为( )
A.9.5万件
B.9万件
C.9500件
D.5000件难度: 中等查看答案及解析
-
3的倒数是( )
A.-3
B.3
C.
D.难度: 中等查看答案及解析
-
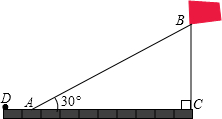
如图,平放在台面上的圆锥体的主视图是( )

A.
B.
C.
D.难度: 中等查看答案及解析
-
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
化简
的结果是( )
A.
B.
C.
D.难度: 中等查看答案及解析
-
班长去文具店买毕业留言卡50张,每张标价2元,店老板说可以按标价九折优惠,则班长应付( )
A.45元
B.90元
C.10元
D.100元难度: 中等查看答案及解析
-
二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )
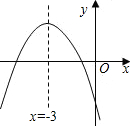
A.y1<y2
B.y1=y2
C.y1>y2
D.不能确定难度: 中等查看答案及解析
-
不等式组
的整数解是( )
A.1,2
B.1,2,3
C.
D.0,1,2难度: 中等查看答案及解析
-
如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则DE的长度是( )
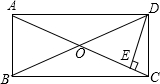
A.3
B.5
C.
D.难度: 中等查看答案及解析