-
设集合
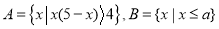 ,若
,若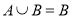 ,则
,则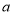 的值可以是( )
的值可以是( )A.
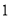 B.
B.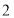 C.
C.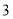 D.
D.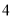
难度: 简单查看答案及解析
-
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图,会标是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形的一个锐角为
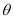 ,且
,且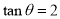 ,若在大正方形内随机取一点,则该点取自小正方形区域的概率为( )
,若在大正方形内随机取一点,则该点取自小正方形区域的概率为( )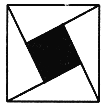
A.
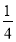 B.
B. 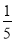
C.
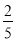 D.
D. 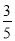
难度: 中等查看答案及解析
-
已知
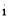 为虚数单位,
为虚数单位,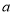 为实数,复数
为实数,复数 在复平面内对应的点为
在复平面内对应的点为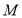 ,则“
,则“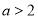 ”是“点
”是“点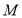 在第四象限”的( )
在第四象限”的( )A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
难度: 简单查看答案及解析
-
已知奇函数
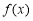 ,当
,当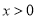 时单调递增,且
时单调递增,且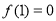 ,若
,若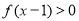 ,则
,则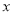 的取值范围为( )
的取值范围为( )A.
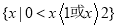 B.
B.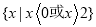
C.
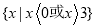 D.
D.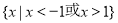
难度: 中等查看答案及解析
-
已知
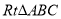 ,点
,点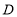 为斜边
为斜边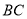 的中点,
的中点,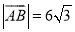 ,
,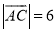 ,
,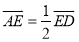 ,则
,则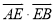 等于( )
等于( )A.-14 B.-9 C.9 D.14
难度: 中等查看答案及解析
-
执行如图所示的程序框图,输出的
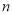 值为
值为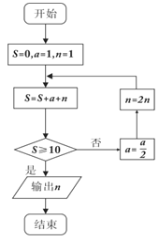
A.
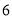 B.
B.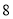
C.
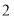 D.
D.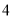
难度: 中等查看答案及解析
-
学校组织同学参加社会调查,某小组共有5名男同学,4名女同学。现从该小组中选出3位同学分别到
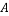 ,
,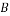 ,
,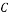 三地进行社会调查,若选出的同学中男女均有,则不同安排方法有( )
三地进行社会调查,若选出的同学中男女均有,则不同安排方法有( )A.70种 B.140种 C.420种 D.840种
难度: 简单查看答案及解析
-
将函数
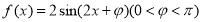 的图象向左平移
的图象向左平移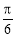 个单位后得到函数
个单位后得到函数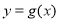 的图象,若函数
的图象,若函数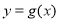 为偶函数,则函数
为偶函数,则函数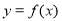 在
在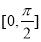 的值域为( )
的值域为( )A.
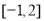 B.
B.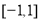 C.
C.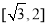 D.
D.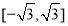
难度: 中等查看答案及解析
-
在棱长为1的正方体中
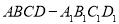 ,点
,点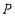 在线段
在线段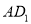 上运动,则下列命题错误的是 ( )
上运动,则下列命题错误的是 ( )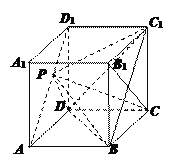
A.异面直线
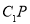 和
和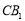 所成的角为定值 B.直线
所成的角为定值 B.直线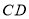 和平面
和平面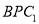 平行
平行C.三棱锥
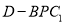 的体积为定值 D.直线
的体积为定值 D.直线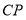 和平面
和平面 所成的角为定值
所成的角为定值难度: 中等查看答案及解析
-
将函数
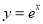 (
(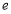 为自然对数的底数)的图象绕坐标原点
为自然对数的底数)的图象绕坐标原点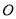 顺时针旋转角
顺时针旋转角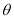 后第一次与
后第一次与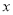 轴相切,则角
轴相切,则角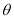 满足的条件是( )
满足的条件是( )A.
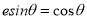 B.
B.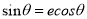 C.
C.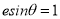 D.
D.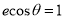
难度: 中等查看答案及解析
-
已知双曲线
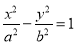
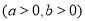 的左,右焦点分别为
的左,右焦点分别为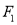 ,
,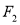 ,点
,点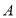 为双曲线右支上一点,线段
为双曲线右支上一点,线段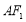 交左支于点
交左支于点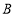 .若
.若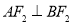 ,且
,且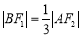 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A.
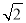 B.
B. 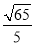 C.
C. 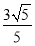 D.
D. 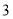
难度: 困难查看答案及解析
-
已知函数
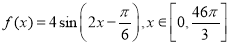 ,若函数
,若函数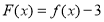 的所有零点依次记为
的所有零点依次记为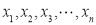 ,且
,且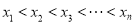 ,则
,则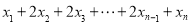 =( )
=( )A.
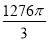 B.
B.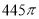 C.
C.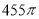 D.
D.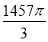
难度: 困难查看答案及解析
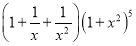 展开式中
展开式中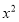 的系数为________.
的系数为________.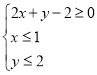 的解集为
的解集为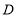 ,若
,若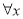 、
、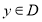 ,
,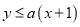 ,则实数
,则实数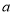 的最小值是______.
的最小值是______.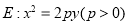 的焦点为
的焦点为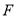 ,
,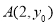 是
是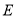 上一点,且
上一点,且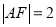 ,设点
,设点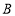 是
是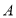 的一点,直线
的一点,直线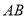 与直线
与直线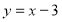 交于点
交于点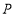 ,过点
,过点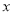 轴的垂线交
轴的垂线交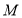 则直线
则直线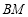 过定点,定点坐标为__________.
过定点,定点坐标为__________.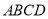 中,
中,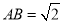 ,
,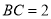 ,
,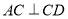 ,
,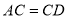 ,则四边形
,则四边形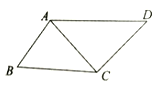
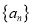 前
前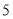 项和为
项和为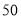 ,
,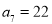 ,数列
,数列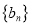 的前
的前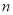 项和为
项和为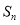 ,
,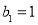 ,
,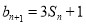 .
.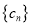 满足
满足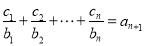 ,
,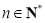 ,求
,求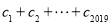 的值
的值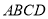 中,
中,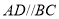 ,
,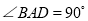 ,
,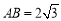 ,
,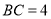 ,
,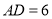 ,
,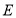 是
是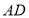 上的点,
上的点,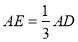 ,
,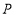 为
为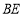 的中点.将
的中点.将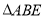 沿
沿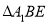 的位置,使得
的位置,使得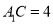 .
.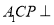 平面
平面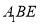 ;
;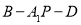 的正弦值.
的正弦值.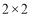 列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?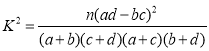
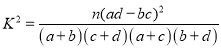
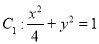 的左、右顶点为
的左、右顶点为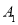 ,
,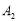 ,上、下顶点为
,上、下顶点为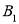 ,
,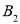 ,记四边形
,记四边形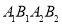 的内切圆为
的内切圆为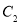 .
.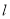 交椭圆
交椭圆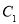 于P,M两点.
于P,M两点.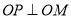 ;
;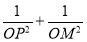 是否为定值.
是否为定值.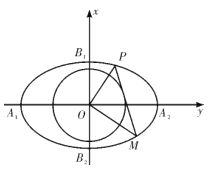
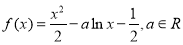 .
.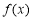 在区间
在区间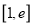 (
(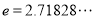 为自然对数的底数)上有唯一的零点,求实数
为自然对数的底数)上有唯一的零点,求实数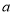 的取值范围;
的取值范围;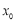 ,使得
,使得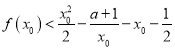 成立,求实数
成立,求实数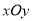 中,以坐标原点为极点,
中,以坐标原点为极点,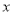 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线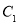 的极坐标方程为
的极坐标方程为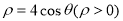 .
.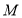 为曲线
为曲线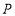 在射线
在射线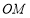 上,且满足
上,且满足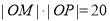 .
.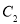 的直角坐标方程;
的直角坐标方程;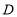 ,过点
,过点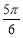 的直线
的直线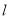 与
与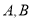 两点,求
两点,求 的值.
的值.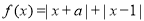 .
.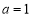 时,求不等式
时,求不等式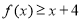 的解集;
的解集;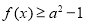 恒成立,求实数
恒成立,求实数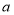 的取值范围.
的取值范围.