-
全集
,
,
,则
( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
已知
为虚数单位,若
,则
( )
A. 1 B.
C.
D. 2
难度: 简单查看答案及解析
-
下列说法中,正确的是( )
A. 命题“若
,则
”的逆命题是真命题
B. 命题“存在
”的否定是:“任意
”
C. 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题
D. 已知
,则“
”是“
”的充分不必要条件
难度: 简单查看答案及解析
-
设函数
则
的值为( )
A. 3 B. 6 C. 8 D. 12
难度: 简单查看答案及解析
-
圆
的一条切线与圆
相交于
,
两点,
为坐标原点,则
( )
A.
B.
C. 2 D.
难度: 简单查看答案及解析
-
已知抛物线
,斜率为
的直线交抛物线于
,
两点.若以线段
为直径的圆与抛物线的准线切于点
,则点
到直线
的距离为( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
我国南宋时期的数学家秦九韶(约1202-1261)在他的著作(数书九章)中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的
,
,
,则程序框图计算的结果为( )
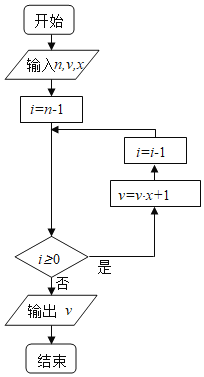
A. 15 B. 31 C. 63 D. 127
难度: 中等查看答案及解析
-
某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
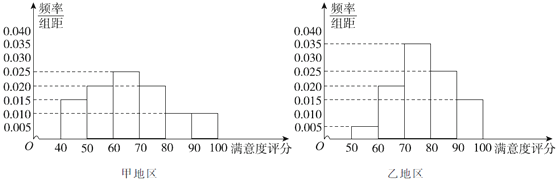
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面正确的是( )
A. m1>m2,s1>s2 B. m1>m2,s1<s2
C. m1<m2,s1<s2 D. m1<m2,s1>s2
难度: 简单查看答案及解析
-
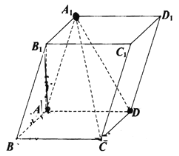
已知四棱锥
的三视图如图所示,则四棱锥
外接球的表面积是( )
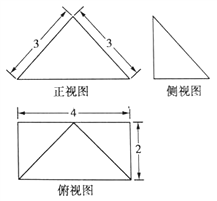
A.
B.
C.
D.
难度: 困难查看答案及解析
-
已知双曲线
的右焦点为
,直线
经过点
且与双曲线的一条渐近线垂直,直线
与双曲线的右支交于不同两点
,
,若
,则该双曲线的离心率为( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
如图,四边形
内接于圆
,若
,
,
,则
的最大值为( )
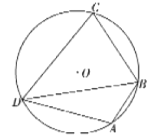
A.
B.
C.
D.
难度: 中等查看答案及解析
-
已知函数
有两个零点
,
,则下列判断:①
;②
;③
;④有极小值点
,且
.则正确判断的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
难度: 中等查看答案及解析
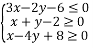 ,则
,则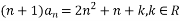 .
.
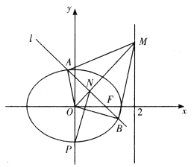
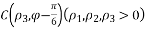 都在曲线
都在曲线