-
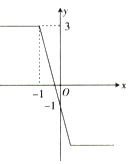
已知集合
,
,则
( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
若
,则复数
在复平面内对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
难度: 简单查看答案及解析
-
为比较甲、乙两名高二学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
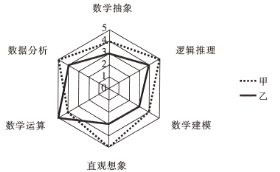
A. 乙的数据分析素养优于甲
B. 乙的数学建模素养优于数学抽象素养
C. 甲的六大素养整体水平优于乙
D. 甲的六大素养中数据分析最差
难度: 简单查看答案及解析
-
已知点
,
是抛物线
:
上的两点,且线段
过抛物线
的焦点
,若
的中点到
轴的距离为2,则
( )
A. 2 B. 4 C. 6 D. 8
难度: 简单查看答案及解析
-
已知向量
,
满足
,且
,
,则向量
与
的夹角为( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
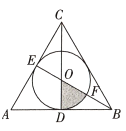
如图,
,
分别是边长为4的等边
的中线,圆
是
的内切圆,线段
与圆
交于点
.在
中随机取一点,则此点取自图中阴影部分的概率是( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
若实数
,
满足约束条件
,设
的最大值与最小值分别为
,
,则
( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
各项均为正数的等比数列
的前
项和为
,若
则
( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
若某几何体的三视图如图所示,则该几何体的所有侧面和底面中,面积的最大值为( )
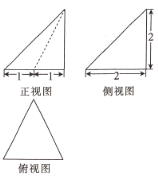
A. 2 B.
C. 3 D.
难度: 中等查看答案及解析
-
已知
是定义在
上的函数,且
,如果当
时,
,则
( )
A. 27 B. -27 C. 9 D. -9
难度: 中等查看答案及解析
-
在平面直角坐标系
中,过双曲线
上的一点
作两条渐近线的平行线,与两条渐近线的交点分别为
,
,若平行四边形
的面积为3,则该双曲线的离心率为( )
A.
B.
C.
D.
难度: 困难查看答案及解析
-
设函数
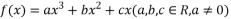 .若不等式
.若不等式对一切
恒成立,则
的取值范围为( )
A.
B.
C.
D.
难度: 困难查看答案及解析
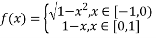 的图象与
的图象与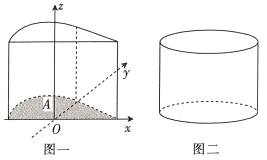
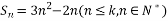 ,现从这
,现从这
 (
(