-
设集合
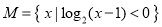 ,集合
,集合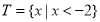 ,则
,则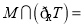 ( )
( )A.
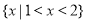 B.
B.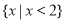 C.
C.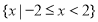 D.
D.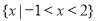
难度: 简单查看答案及解析
-
已知
 为虚数单位,
为虚数单位,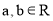 ,若
,若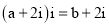 ,则
,则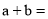 ( )
( )A.
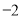 B.0 C.2 D.4
B.0 C.2 D.4难度: 中等查看答案及解析
-
甲乙两名同学分别从“象棋”、“文学”、“摄影”三个社团中随机选取一个社团加入,则这两名同学加入同一个社团的概率是( )
A.
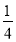 B.
B.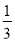 C.
C.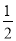 D.
D.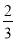
难度: 简单查看答案及解析
-
如图为厦门市2018年国庆节7天假期的楼房认购量与成交量的折线图,请你根据折线图对这7天的认购量(单位:套)与成交量(单位:套),则下列选项中正确的是( )
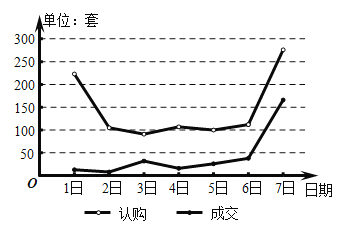
A.日成交量的中位数是10
B.日成交量超过日平均成交量的有2天
C.认购量与日期正相关
D.10月7日认购量的增长率小于10月7日成交量的增长率
难度: 简单查看答案及解析
-
已知双曲线的渐近线方程为
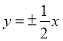 ,焦距为
,焦距为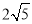 ,则该双曲线的标准方程是( )
,则该双曲线的标准方程是( )A.
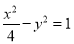 B.
B.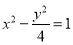 C.
C.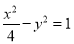 或
或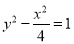 D.
D.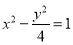 或
或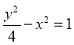
难度: 中等查看答案及解析
-
已知数列
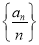 的前n项和为
的前n项和为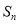 ,且满足
,且满足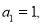
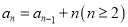 ,则
,则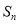 等于( )
等于( )A.
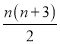 B.
B.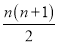 C.
C.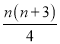 D.
D.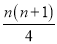
难度: 中等查看答案及解析
-
把函数
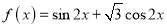 的图象向右平移
的图象向右平移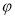 个单位,再把所得图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位,再把所得图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数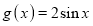 的图象,则
的图象,则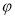 的一个可能值为( )
的一个可能值为( )A.
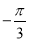 B.
B.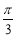 C.
C.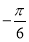 D.
D.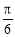
难度: 中等查看答案及解析
-
已知函数
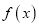 的图象如图所示,则该函数的解析式可能是( )
的图象如图所示,则该函数的解析式可能是( )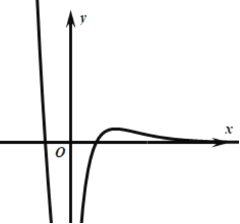
A.
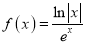 B.
B.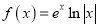 C.
C.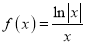 D.
D.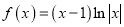
难度: 简单查看答案及解析
-
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体外接球的表面积是( )
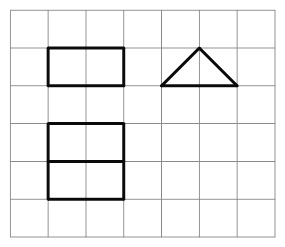
A.
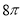 B.
B. C.
C.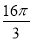 D.
D.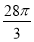
难度: 中等查看答案及解析
-
已知
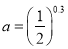 ,
,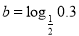 ,
,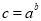 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )A.
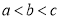 B.
B.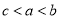 C.
C.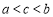 D.
D.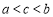
难度: 中等查看答案及解析
-
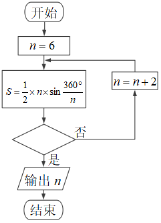
公元263年左右,我国魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率近似值的方法.如图是利用刘徽的割圆术”思想设汁的一个程序框图,若输出
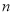 的值为24,则判断框中填入的条件可以为( )
的值为24,则判断框中填入的条件可以为( )(参考数据:
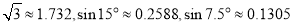 )
)
A.
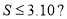 B.
B.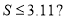 C.
C.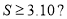 D.
D.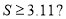
难度: 中等查看答案及解析
-
如图,正方体
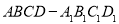 的棱长为
的棱长为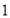 ,
,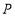 为
为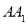 的中点,
的中点,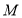 在侧面
在侧面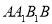 上,若
上,若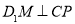 ,则
,则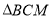 面积的最小值为( )
面积的最小值为( )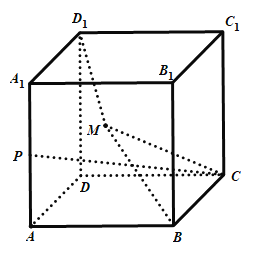
A.
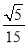 B.
B. C.
C.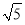 D.
D.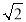
难度: 中等查看答案及解析
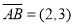 ,
,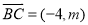 ,且
,且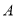 ,
,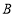 ,
,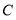 三点共线,则
三点共线,则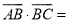 _______.
_______.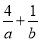 的最小值是
的最小值是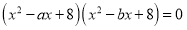 四个不同根按一定顺序排序后可以组成首项为1的等比数列,则
四个不同根按一定顺序排序后可以组成首项为1的等比数列,则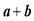 的值为________.
的值为________.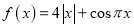 ,对于
,对于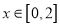 都有
都有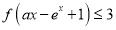 ,则实数a的取值范围是________.
,则实数a的取值范围是________.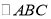 中,角A,B,C的对边分别为a,b,c,已知
中,角A,B,C的对边分别为a,b,c,已知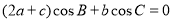 .
.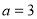 ,点D在AC边上且
,点D在AC边上且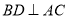 ,
,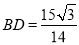 ,求c.
,求c.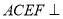 平面
平面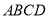 ,四边形
,四边形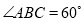 ,
,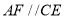 ,
,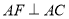 ,
,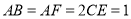 .
.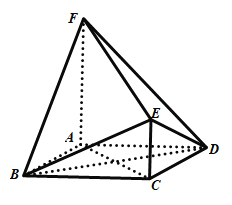
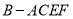 的体积;
的体积;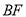 上有一点
上有一点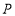 ,使得
,使得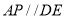 ,求
,求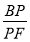 的值.
的值.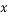 (单位:亿元)对年销售额
(单位:亿元)对年销售额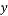 (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①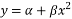 ,②
,②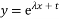 ,其中
,其中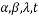 均为常数,
均为常数, 为自然对数的底数.
为自然对数的底数.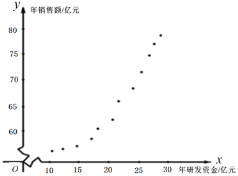
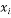 和年销售额
和年销售额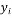 的数据,
的数据,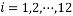 ,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令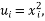
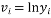
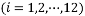 ,经计算得如下数据:
,经计算得如下数据: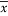
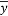
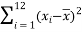
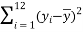
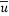
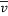
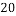
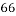
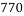
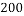
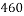
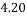
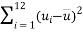
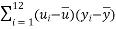
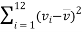
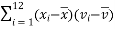
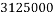
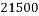
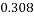
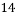
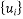 和
和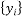 的相关系数为
的相关系数为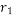 ,
,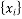 和
和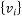 的相关系数为
的相关系数为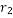 ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;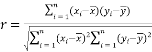 ,回归直线
,回归直线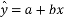 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: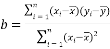 ,
,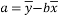 ;
;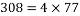 ,
,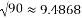 ,
,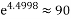 .
.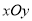 中,
中,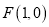 ,动点
,动点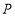 满足:以
满足:以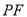 为直径的圆与
为直径的圆与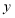 轴相切.
轴相切.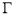 ,直线
,直线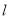 过点
过点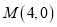 且与
且与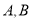 两点,当
两点,当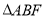 与
与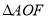 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线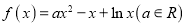 .
.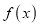 的单调性;
的单调性;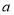 的范围.
的范围.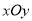 中,直线
中,直线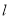 的参数方程为
的参数方程为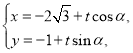 (
(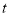 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,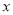 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线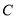 的极坐标方程为
的极坐标方程为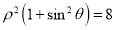 .
.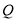 的极坐标为
的极坐标为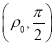 ,且
,且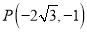 ,
,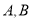 ,求
,求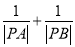 的最大值.
的最大值.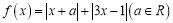 .
.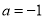 时,求不等式
时,求不等式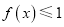 的解集;
的解集;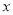 的不等式
的不等式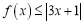 的解集为
的解集为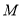 ,且
,且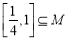 ,求
,求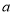 的取值范围.
的取值范围.