已知平面向量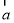 ,
,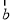 ,
,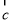 满足
满足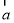 与
与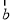 的夹角为锐角,
的夹角为锐角,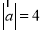 ,
,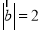 ,
,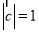 ,且
,且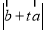 的最小值为
的最小值为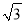 ,则实数
,则实数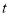 的值是_____,向量
的值是_____,向量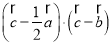 的取值范围是_____.
的取值范围是_____.
高一数学填空题困难题
已知平面向量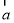 ,
,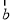 ,
,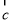 满足
满足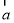 与
与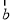 的夹角为锐角,
的夹角为锐角,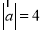 ,
,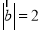 ,
,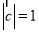 ,且
,且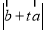 的最小值为
的最小值为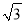 ,则实数
,则实数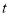 的值是_____,向量
的值是_____,向量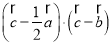 的取值范围是_____.
的取值范围是_____.
高一数学填空题困难题
关于平面向量,下列结论正确的个数为( )
①若,则
;
②若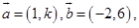
∥
,则
;
③非零向量和
满足
则
与
的夹角为30°;
④已知向量,且
与
的夹角为锐角,则实数
的取值范围是
.
A. 4个 B. 3个 C. 2个 D. 1个
高一数学选择题中等难度题查看答案及解析
关于平面向量,下列结论正确的个数为( )
①若,则
;
②若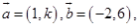
∥
,则
;
③非零向量和
满足
则
与
的夹角为30°;
④已知向量,且
与
的夹角为锐角,则实数
的取值范围是
.
A. 4个 B. 3个 C. 2个 D. 1个
高一数学选择题中等难度题查看答案及解析
给出下列命题:(1)、
是锐角
的两个内角,则
;(2)在锐角
中,
则
的取值范围为 (
);(3)已知
为互相垂直的单位向量,
且
的夹角为锐角,则实数
的取值范围是
;(4)已知O是
所在平面内定点,若P是
的内心,则有
;(5)直线x= -
是函数y=sin(2x-
)图象的一条对称轴。其中正确命题是( )
A 。(1)(3)(5) B。 (2)(4)(5) C。 (2)(3)(4) D。(1) (4) (5)
高一数学选择题困难题查看答案及解析
已知两个不共线的向量的夹角为
,且
为正实数.
(1)若与
垂直,求
;
(2)若,求
的最小值及对应的
的值,并指出此时向量
与
的位置关系.
(3)若为锐角,对于正实数
,关于
的方程
有两个不同的正实数解,且
,求
的取值范围.
【答案】(1) ;(2)答案见解析;(3)
.
【解析】试题分析:(1)利用+2
与
﹣4
垂直,(
+2
)•(
﹣4
)=0,可得,化简,即可求出tanθ;
(2)利用二次函数的性质,可求|x﹣
|的最小值及对应的x的值,利用数量积公式,可确定向量
与x
﹣
的位置关系;
(3)方程|x﹣
|=|m
|,等价于9x2﹣3cosθx+1﹣9m2=0,利用关于x的方程|x
﹣
|=|m
|有两个不同的正实数解,建立不等式,即可确定结论.
(1)由题意,得即
故
又
,故
因此, 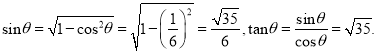
(2)
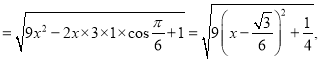 故当
故当时,
取得最小值为
此时,
故向量与
垂直.
(3)对方程两边平方,得
①
设方程①的两个不同正实数解为,则由题意,得
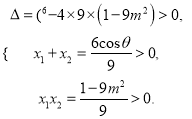 ,
,
解之,得
若则方程①可以化为
,
则即
由题知
故
令,得
,故
,且
.
当,且
时,
的取值范围为
,且
};
当,或
时,
的取值范围为
.
【题型】解答题
【结束】
22
已知向量,设函数
.
(1)若函数的图象关于直线
对称,
,求函数
的单调递增区间;
(2)在(1)的条件下,当高一数学解答题中等难度题查看答案及解析
下列命题:
①若,则
;
②已知,
,且
与
的夹角为锐角,则实数
的取值范围是
;
③已知是平面上一定点,
是平面上不共线的三个点,动点
满足
,
,则
的轨迹一定通过
的重心;
④在中,
,边长
分别为
,则
只有一解;
⑤如果△ABC内接于半径为的圆,且
则△ABC的面积的最大值;
其中正确的序号为_______________________。
高一数学填空题中等难度题查看答案及解析
已知向量,
.若向量
与
的夹角为锐角,则实数
的取值范围为______.
高一数学填空题简单题查看答案及解析
已知,向量
与向量
的夹角锐角,则实数
的取值范围是 .
高一数学填空题简单题查看答案及解析
高一数学填空题中等难度题查看答案及解析
已知,向量
与向量
的夹角锐角,则实数
的取值范围是
高一数学填空题简单题查看答案及解析
已知,向量
与向量
的夹角锐角,则实数
的取值范围是
高一数学填空题简单题查看答案及解析