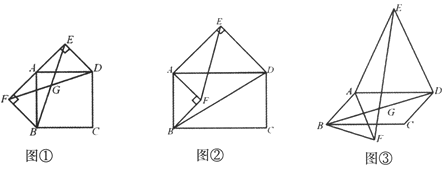
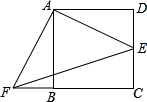
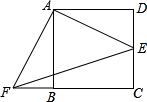
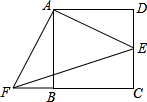
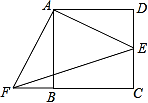
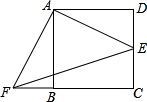
以四边形ABCD的边AB、AD为底边分别作等腰三角形ABF和ADE,连接EB.
(1)当四边形ABCD为正方形时(如图1),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EB和FD的数量关系是 .
(2)当四边形ABCD为矩形时(如图2),以边AB、AD为斜边分别向内侧作等腰直角三角形ABF和ADE,连接EF、BD,线段EF和BD具有怎样的数量关系?请加以证明;
(3)当四边形ABCD为平行四边形时(如图3),以边AB、AD为斜边分别向平行四边形内测、外侧作等腰直角三角形ABF和ADE,且△EAD与△FBA的顶角都为α,连接EF、BD,交点为G,请用α表示出∠EGD,并说明理由.

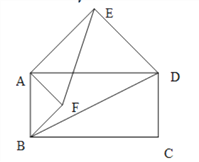
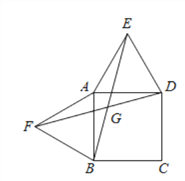
图1 图2 图3
【答案】(1)EF=BD;(2)EF=BD;(3)
【解析】分析:(1)正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△AFD≌△ABE,由全等三角形的性质即可得到EB=FD;(2)根据等腰直角三角形的性质可得,再证得∠BAD=∠FAE,即可判定△BAD∽△FAE ,根据相似三角形的性质可得
,即可得
;(3)
,先证△BFA∽△DEA,即可得
,
再证得,所以△BAD∽△FAE,根据全等三角形的性质即可得
,再由∠AHE=∠DHG,即可得
.
详【解析】
(1)EF=BD,
理由如下:
四边形ABCD为正方形,
∴AB=AD,
∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中, ,
∴△AFD≌△ABE,
∴EB=FD;
(2)EF=BD.
证明:∵△AFB为等腰直角三角形
∴,∠FAB=45°
同理: ,∠EAD=45° ∴∠BAD+∠FAD=∠EAD+∠DAF
即∠BAD=∠FAE
∵,
∴
∴△BAD∽△FAE ∴
即:
(3)【解析】
∵△AFB为等腰直角三角形,∴FB=FA,
同理:ED=EA,∴,
又∵ ,∴△BFA∽△DEA,
∴,
∴,
∴,
∴△BAD∽△FAE,
∴,
又∵∠AHE=∠DHG,
∴.
点睛:本题考查了正方形的性质、全等三角形的判定和性质、等边三角形的性质等腰直角三角形的先证、相似三角形的判定和性质,题目的综合性很强,难度也不小,解题的关键是对特殊几何图形的性质要准确掌握.
【题型】解答题
【结束】
27
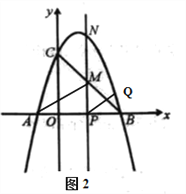
如图,二次函数的图象交x轴于A、B两点,交y轴于点C,点B的坐标为(3,0),顶点C的坐标为(1,4).连接BC.
(1)求二次函数的解析式和直线BC的解析式;
(2)点M是直线BC上的一个动点(不与B、C重合),过点M作x轴的垂线,交抛物线于点N,交x轴于点P.
①如图1,求线段MN长度的最大值;
②如图2,连接AM,QN,QP.试问:抛物线上是否存在点Q,使得与
的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,请说明理由.

九年级数学解答题困难题