猜想与证明:
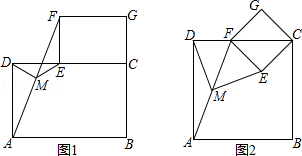
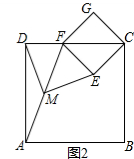
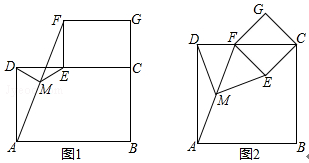
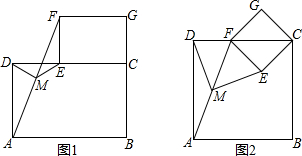
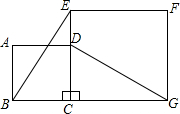
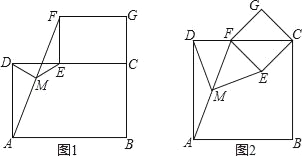
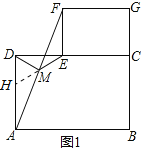
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
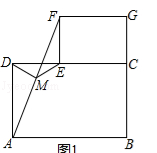
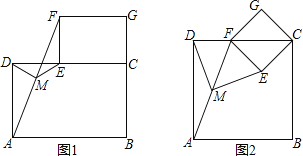
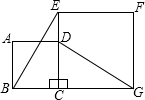
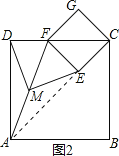
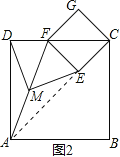
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
【答案】猜想:DM=ME,证明见解析;(2)成立,证明见解析.
【解析】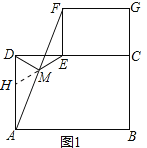
延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.
如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=DE,
∴DM=HM=ME,
∴DM=ME.
(1)、如图1,延长EM交AD于点H,
∵四边形ABCD和CEFG是矩形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM
∴DM=HM=ME,
∴DM=ME,
(2)、如图2,连接AE,
∵四边形ABCD和ECGF是正方形,
∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,
在RT△ADF中,AM=MF,
∴DM=AM=MF,
在RT△AEF中,AM=MF,
∴AM=MF=ME,
∴DM=ME.
考点:(1)、三角形全等的性质;(2)、矩形的性质.
【题型】解答题
【结束】
25
已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

九年级数学解答题困难题