-
已知集合
,
,则( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
“
”的否定是( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
“
”的否定是( )
A.
B.
C.
D.
【答案】D
【解析】“
,
”的否定是
,
,故选D.
【题型】单选题
【结束】
3“
”是“方程
表示焦点在
轴上的椭圆”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
难度: 简单查看答案及解析
-
“
”是“方程
表示焦点在
轴上的椭圆”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】 若方程
表示焦点在
轴上的椭圆,则
,所以
,
所以
是方程
表示焦点在
轴上的椭圆的充分不必要条件,故选A.
【题型】单选题
【结束】
4曲线
与直线
与直线
所围成的封闭图形的面积为( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
曲线
与直线
与直线
所围成的封闭图形的面积为( )
A.
B.
C.
D.
【答案】D
【解析】联立曲线与两条直线的方程组成的方程组可得三个交点分别为
,结合图形可得封闭图形的面积为
,应选答案D。
【题型】单选题
【结束】
5设双曲线
的离心率是
,则其渐近线的方程为( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
设双曲线
的离心率是
,则其渐近线的方程为( )
A.
B.
C.
D.
【答案】D
【解析】双曲线
的离心率是
,
可得
,即
,可得
则其渐近线的方程为
故选
【题型】单选题
【结束】
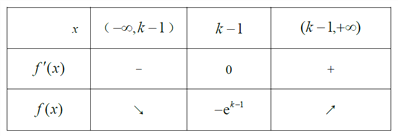
6设函数
在区间
上单调递减,则实数
的取值范围是( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
设函数
在区间
上单调递减,则实数
的取值范围是( )
A.
B.
C.
D.
【答案】C
【解析】∵
,
∴
,
由
得
,
∴函数
的单调减区间为
,
又函数
在区间
上单调递减,
∴
,
∴
,解得
,
∴实数
的取值范围是
.选C.
点睛:已知函数在区间上的单调性求参数的方法
(1)利用导数求解,转化为导函数在该区间上大于等于零(或小于等于零)恒成立的问题求解,一般通过分离参数化为求函数的最值的问题.
(2)先求出已知函数的单调区间,然后将问题转化为所给的区间是函数相应的单调区间的子集的问题处理.
【题型】单选题
【结束】
7设
,函数
的图象向右平移
个单位长度后与原图象重合,则
的最小值是( )
A.
B.
C.
D.
难度: 简单查看答案及解析
-
设
,函数
的图象向右平移
个单位长度后与原图象重合,则
的最小值是( )
A.
B.
C.
D.
【答案】A
【解析】函数
的图象向右平移
个单位长度后所得图象对应的函数解析式为
,
由题意得
,
∴
,
∵
,
∴
的最小值是
.选A.
【题型】单选题
【结束】
8公差不为0的等差数列
中,已知
且
,其前
项和
的最大值为( )
A. 25 B. 26 C. 27 D. 28
难度: 中等查看答案及解析
-
公差不为0的等差数列
中,已知
且
,其前
项和
的最大值为( )
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】设等差数列
的公差为
,
∵
,
∴
,
整理得
,
∵
,
∴
.
∴
,
∴当
时,
.
故
最大,且
.选B.
点睛:求等差数列前n项和最值的常用方法:
①利用等差数列的单调性, 求出其正负转折项,便可求得和的最值;
②将等差数列的前n项和
(A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
【题型】单选题
【结束】
9如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
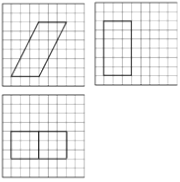
A.
B.
C. 90 D. 81
难度: 中等查看答案及解析
-
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
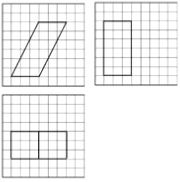
A.
B.
C. 90 D. 81
【答案】B
【解析】由三视图可得,该几何体是一个以俯视图为底面的平行六面体(四棱柱).
其底面的面积为
,
前后两个面的面积为
,
左右两个面的面积为
.
故棱柱的表面积为
.选B.
【题型】单选题
【结束】
10已知实数
满足约束条件
,如果目标函数
的最大值为
,则实数
的值为( )
A. 3 B.
C. 3或
D. 3或
难度: 困难查看答案及解析
-
已知实数
满足约束条件
,如果目标函数
的最大值为
,则实数
的值为( )
A. 3 B.
C. 3或
D. 3或
【答案】D
【解析】先画出线性约束条件所表示的可行域,目标函数化为
,目标函数
的最大值只需直线的截距最大,
当
,
(1)
,即
时,最优解为
,
,符合题意;
(2)
,即
时,最优解为
,
,不符舍去;
当
,
(3)
,即
时,最优解为
,
,符合;
(4)
,即
时,最优解为
,
,不符舍去;
,
,
综上:实数
的值为3或
,选D.
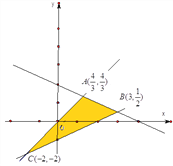
【题型】单选题
【结束】
11在
中,
,若一个椭圆经过
两点,它的一个焦点为点
,另一个焦点在边
上,则这个椭圆的离心率为( )
A.
B.
C.
D.
难度: 中等查看答案及解析
-
在
中,
,若一个椭圆经过
两点,它的一个焦点为点
,另一个焦点在边
上,则这个椭圆的离心率为( )
A.
B.
C.
D.
【答案】C
【解析】
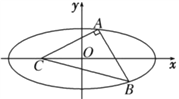
设另一焦点为
中,
,
又
,
在
中焦距
则
故选
点睛:本题主要考查了椭圆的简单性质。设另一焦点为
,则可在
中,根据勾股定理求得
,进而根据椭圆的定义知
,求得
的值,再利用
求得
,最后在
中根据勾股定理求得
,得到焦距,进一步求得离心率。
【题型】单选题
【结束】
12已知函数
,若
成立,则
的最小值为( )
A.
B.
C.
D.
难度: 中等查看答案及解析

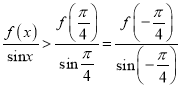 ,
,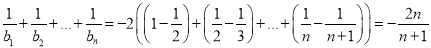
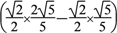 =-
=-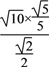 =2,
=2,