已知函数在
与
处都取得极值.
(1)求函数的解析式;
(2)求函数在区间[-2,2]的最大值与最小值.
【答案】(1)(2)最大值2,最小值-6
【解析】
(1)根据所给的函数的解析式,对函数求导,使得导函数等于0,得到关于a,b的关系式,解方程组即可,写出函数的解析式;(2)对函数求导,写出函数的导函数等于0的x的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到结果
(1)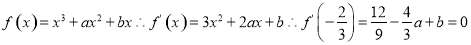
,所以解析式为
(2)由(1)得,由
得增区间为
,由
得减区间为
,
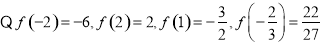 ,所以函数最大值为
,所以函数最大值为,最小值为
考点:1.利用导数求闭区间上函数的最值;2.函数在某点取得极值的条件
【题型】解答题
【适用】较易
【标题】2015-2016学年河北省广平县一中高二上学期第四次月考理科数学试卷(带解析)
【关键字标签】
【结束】
已知函数.
(Ⅰ)当时,求曲线
在
处的切线方程;
(Ⅱ)设函数,求函数
的单调区间;
【答案】(Ⅰ)x+y﹣2=0(Ⅱ)当a>﹣1时,h(x)在(0,a+1)上单调递减,在(a+1,+∞)上单调递增当a≤﹣1时,h(x)在(0,+∞)上单调递增
【解析】
(1)欲求在点x=1处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率;(2)先求出h(x)的导数,根据h′(x)>0求得的区间是单调增区间,h′(x)<0求得的区间是单调减区间,从而问题解决
(Ⅰ)当a=2时,f(x)=x﹣2lnx,f(1)=1,切点(1,1),
∴,∴k=f′(1)=1﹣2=﹣1,
∴曲线f(x)在点(1,1)处的切线方程为:y﹣1=﹣(x﹣1),即x+y﹣2=0.
(Ⅱ),定义域为(0,+∞),
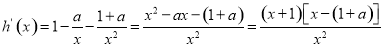
①当a+1>0,即a>﹣1时,令h′(x)>0,
∵x>0,∴x>1+a
令h′(x)<0,∵x>0,∴0<x<1+a.
②当a+1≤0,即a≤﹣1时,h′(x)>0恒成立,
综上:当a>﹣1时,h(x)在(0,a+1)上单调递减,在(a+1,+∞)上单调递增.
当a≤﹣1时,h(x)在(0,+∞)上单调递增.
考点:1.利用导数研究曲线上某点切线方程;2.利用导数研究函数的单调性
【题型】解答题
【适用】较易
【标题】2015-2016学年河北省广平县一中高二上学期第四次月考理科数学试卷(带解析)
【关键字标签】
【结束】
如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
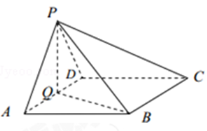
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
【答案】(1)详见解析(2)
【解析】
(1)由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;(2)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC⊂平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出
(1)∵PA=PD,
∴PQ⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,∴BQ⊥AD,PQ∩BQ=Q,
∴AD⊥平面PQB 又AD平面PAD,
∴平面PQB⊥平面PAD;
(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,
∴PQ⊥平面ABCD,BC⊂平面ABCD,∴PQ⊥BC,
又BC⊥BQ,QB∩QP=Q,∴BC⊥平面PQB,
又PM=3MC, ∴VP﹣QBM=VM﹣PQB=
考点:1.面面垂直的判定;2.棱锥的体积
【题型】解答题
【适用】较易
【标题】2015-2016学年河北省广平县一中高二上学期第四次月考理科数学试卷(带解析)
【关键字标签】
【结束】
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
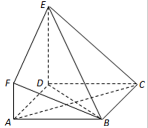
(1)求证:AC⊥平面BDE;
(2)求二面角FBED的余弦值.
高二数学解答题简单题